In Reviewing Chows and Mannings Work Relative to the Velocity

Chezy and Manning developed equations that are used to determine the average volumetric flowrate in open up channels. This article explains a laboratory method that was adult and tested to further identify and quantify the parameters that make up the roughness coefficients of those equations. This method uses a hydraulic flume, and makes use of the technique of dimensional homogeneity and a new exponential course of an equation for musical instrument calibration.

Accurately measuring average velocities in channels or culverts with surfaces open to the atmosphere has been a claiming for centuries. The larger the period cross-sectional area the greater the inaccuracy or uncertainty of measurement.

Open up-channel flow is governed past the Froude relation, the ratio of inertial forces to gravitational forces. Thus, it was recognized early on in the history of hydraulics that the formula for such average velocity would need to exist a balance between gravity, causing the flow, and channel roughness, seeking to retard the flow. Information technology was also recognized that any such formula would have to be for uniform menstruation, that is, for steady state menstruation, such that the water depth relative to the bottom of the waterway is a constant, or d(y)/dx = 0.

It is noted that in pipe or pressurized flow the give-and-take compatible has a different meaning. In that application, it means that the velocity contour has a constant velocity over the entire cross-section. On the other hand, open up-channel hydraulics has no word for constant velocity over a cross-department. In this article, "normal" ways the start of these 2 definitions, that is, steady state and abiding depth. All units in this article are engineering units as commonly used in the U.S.

Equations Adult by Chezy and Manning

The first recognized and most lasting "resistance" formula for steady state, open-channel flow is credited to Antoine Chezy. He was tasked with determining the cross-section and calculating the discharge for the Paris h2o supply, and increasing its flowrate. He did and then in 1768 by comparison flow weather between two water courses, the Courpalet Canal and the Seine River. His resulting formula was published in his report on the Canal de fifty'Yvette as:

V_avg = C 10 R^1/2 x S^1/2

where V_avg is the average velocity in anxiety per second; C is Chezy'south cistron of menstruation resistance in feet^1/2/sec; R is the hydraulic radius (the cross-sectional expanse divided by the wetted perimeter) in feet; and S is the gradient, which is dimensionless. However, Chezy's piece of work received little attention until many years later his expiry.

In 1889, an Irishman named Robert Manning, who was Master Engineer of Republic of ireland's Office of Public Works, presented a newspaper entitled "On the Period of Water in Open Channels and Pipes." Although his main interest appears to have been hydrology, he derived an average "resistance" formula for open channels from all the dissimilar resistance formulas published upward to that time. In today's format, this equation, which we'll phone call Equation ane for future reference, is:

V_avg = (ane.486/northward) ten R^2/three x S^1/two

where n is Manning'south roughness coefficient, which is the same numerically in either U.S. or metric dimensional systems. In the U.S. arrangement, it has units of 2d/feet^1/3. If using metric units, the ane.486 is replaced by 1.0 and its units are second/meter^1/3.

Manning'southward equation has been the most successful of all open-channel empirical equations, based on the resistance to catamenia and derived from observation. In fact, it is no exaggeration to say it is the cornerstone of today'due south science of hydraulic applied science.

However, in the classic sense, both Chezy'southward and Manning's equations have several similar shortcomings. First, they practise not have dimensional homogeneity, that is, the units on the left side are not the same every bit the units on the right side. Such equations are usually derived past experimentation or ascertainment and rapidly lose accuracy if extrapolated across their range of observation. Information technology is known that Manning'southward equation loses accuracy with very steep or shallow slopes. Secondly, to reach dimensional homogeneity, their constants or coefficients are not pure numbers, simply are artificially assigned units.

Furthermore, Manning's equation suggests the boilerplate velocity is more sensitive to the hydraulic radius than to the slope. This actually is an incompatibility, because the very nature of open-channel flow is a function of the slope component of gravity. The shape of the water passage, every bit calculated by the hydraulic radius, does exert an effect on the absolute roughness, but it is not a principal effect on the average velocity itself. The lower the hydraulic radius ratio, the greater the percentage of the flow that is in contact with the roughness of the boundaries.

Additionally, the very nature of the equations is a contradiction. The equations describe an average velocity that exists at a cantankerous-department perpendicular to the menstruum. Such a cross-section has an infinitesimal thickness in the direction of menstruum, while the equations rely on coefficients that are referred to as "roughness coefficients." But the effect of such roughness needs a finite length to be—information technology cannot have an effect over an infinitesimal thickness. This means the roughness itself must act on some other parameter that can exist over an infinitesimal length to retard the period velocity.

Theory Behind a Laboratory Experiment

The accuracies of both Chezy's and Manning's equations depend on the selection of their individual roughness coefficients. This is usually done by comparison with known similar streams or from a reference volume of pictures of streams. However, in the article titled "Dimensionally Homogeneous Form of the Chezy and Manning Equations," published by Hydro Review in Apr 2014, I proposed a new experimental method of determining the constituent parts that comprise these roughness coefficients.

To demonstrate the technique, I presented to a graduate course in Renewable Energy Engineering enrolled in the Hydraulic Laboratory course at the Oregon Institute of Engineering (OIT) in Wilsonville, Oregon, an experiment designed to place and quantify the components of the roughness coefficients. This experiment would concentrate on Manning's equation, and was based on using the principle of dimensional homogeneity. The OIT graduate students who participated in this laboratory experiment were Joshua Couch, Cole Harrington, Karissa Hilsinger, Tai Huynh, Krystal Locke, William Perreira, Cullen Ryan, Pauloi Santos Vasconcelos Jr., Anurak Sitthiwong, and Asmitha Velivela.

First, two parameters were formed: H_v/S and R. H₅ represents the velocity head, that is, H_v = (α 10 V_avg ²) / (ii x grand), where α is called the velocity caput correction gene or the Coriolis factor. This multiplier represents the additional energy independent in either open-surface or closed-pressure period that exists whenever a velocity profile is not constant over a cross-sectional area. This is because fluid energy is a office of the foursquare of the velocity, and the sum of the squares in each fluid stream tube is greater than the square of the sum of the velocities in each stream tube.

Numerically α is always equal to or greater than one and is dimensionless. The slope or S could accept appeared on either parametric side, but was assigned to the H_five parameter, because in hydraulics at that place is more than ample show that the average velocity is a part of the square root of the slope, that is, V_avg ≈ S^ane/2. Then, a laboratory experiment was designed that would permit data to be obtained and plotted as H₅/S versus R, both of which have units of feet. Therefore, any resulting experimental equation should accept dimensional homogeneity.

The units of H_v, from Bernoulli's equation, are foot-pounds per pound or "specific energy," but are withal homogeneous with R, which has units of feet. Information technology is to exist noted that every bit R gets larger, the wetted perimeter (P) gets smaller relative to the area (A). This means frictional resistance to flow must go smaller, and therefore, the average velocity should get larger. In other words, a linear relation between H_v/Southward and R should have a positive slope.

Test Apparatus

A pocket-sized tiltable-bed laboratory flume with a swimming pool recirculating pump, which 1 student had conveniently built the prior semester, was adapted for use. It was immediately evident that measuring the velocity caput correction gene in such a minor flume would exist impossible. The best alternative was to only measure gradient, boilerplate velocity, and h2o depth for critical and uniform period.

At disquisitional period, where the Froude number is equal to one, the least hydraulic energy is independent for a given quantity of moving fluid. Consequently, there should not be any boosted energy available to grade a non-constant velocity contour and the velocity caput correction factor should be most one. In addition, because the flume was brusk, the energy in the fluid inbound the flume needed to exist matched to the free energy level desired for a given flowrate in the flume, so that uniform or steady land period was immediately accomplished.

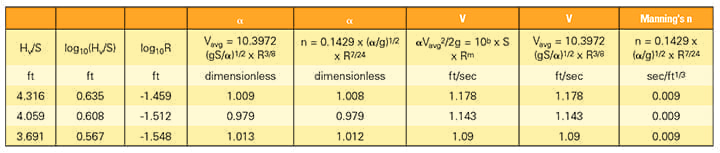
It was not possible to conform the swimming puddle pump that finely. Consequently, the squad of researchers opted to bring in a 2nd water tank, have the pump belch into that tank, and and then advisedly siphon from that tank into the flume. A sonic flowmeter connected to the hose between the tank and flume gave the volumetric flowrate. It took a considerable amount of time and effort to become everything counterbalanced for a single data bespeak of steady state, uniform, and critical flow in such a small flume. However, ultimately three information points were collected, which were sufficient to demonstrate this method of data analysis (Tables ane and ii).

Tabular array i. This table shows data collected during three open-aqueduct experiments conducted in the lab using a flume. Source: Lee H. Sheldon, PE

Table 2. This table shows data collected during three open-channel experiments conducted in the lab using a flume. Source: Lee H. Sheldon, PE

It is emphasized these data points were closely spaced in terms of volumetric flowrate. This is considering a 5-inch-wide flume—operated for both uniform and critical flows—did not provide for a wide range of period variability. Also, this experiment was washed in a very smoothen Plexiglas flume where Manning's north was measured every bit simply 0.009, whereas, 0.012 is the smoothest value in the published tabular array of prototype water canals. Therefore, any numerical results should be viewed as applying merely to this very narrow hydraulic government.

Withal, information technology is also emphasized that the objective of this laboratory experiment was just to demonstrate whether this method could exist used in time to come, more-extensive enquiry to provide further insight and accuracy into the makeup of the components of Chezy's and particularly Manning'south equations.

Data Reduction Technique

The plotting of these 3 data points was washed in the aforementioned manner equally the instrument scale equation described in an commodity I wrote titled "A New Calibration Equation for the Winter-Kennedy Piezometer Organisation," which was published past Hydro Review in October 2013. This method yields a calibration equation directly in exponential form for ready comparison with the ordinarily used open-channel equations, that is, log_x(H_v/S) was plotted every bit the ordinate or y-axis and log_tenR was plotted as the abscissa or x-axis (Effigy 1).

1. This chart shows the model flume at critical and uniform catamenia. Source: Lee H. Sheldon, PE

These points closely approximated a straight line and yielded an equation of the course: y = mx + b.

log₁₀(H_five/Southward) = mlog₁₀R + b = log₁₀(R^m) + b

Raising both sides of the equation as powers of x yields:

10^(log_tenH_v/S) = 10^(log_tenR^m + b) = 10^b x 10^(log₁₀R^m)

Then, by logarithmic identity:

H_five/S = 10^b x R^{one thousand}

or

H_five = 10^b x S x R^m

Substituting for H_v results in:

αV_avg ⁱⁱ/2g = 10^b x S x R^m

Rearranging terms gives:

V_avg = (2g10^b/α)^1/2 ten S^i/2 x R^m/2

Substituting numerical values of m = 0.7497 and b = 1.7328 from Figure i provides:

V_avg = (2g x x^1.7328/α)^1/2 x Southward^1/2 10 (R^0.7497)^1/2

It is noted that the gradient (m) is positive equally predicted earlier. Therefore:

5_avg = (108.1011g/α)^ane/2 x S^1/ii x R^0.3749

Resulting in the following equation, which we'll call Equation 2 for future reference:

Five_avg = x.3972(gS/α)^1/ii x R^3/eight

Now, in this form, the open up-channel equation contains but parameters that may exist determined beyond an infinitely thin cantankerous-sectional area. Comparing Equation 2 with Equation 1 provides insight into the relationships of the parameters in Manning'due south equation.

V_avg = 10.3972 x (gS/α)^i/2 ten R^three/viii = (one.486/north) 10 R^2/3 x S^1/2

Now, equating just the ii expressions and canceling the S^i/ii terms gives:

10.3972 ten (grand/α)^1/2 x R^3/8 = (1.486/n) x R^ii/iii

Combining the R terms, results in:

10.3972 x (g/α)^1/2 = (1.486/n) 10 R^7/24

Which results in the following, which nosotros'll telephone call Equation 3 for hereafter reference:

= 0.1429 10 (α/yard)^one/2 ten R^7/24

It is noted that Equation ii does not have exact dimensional homogeneity. Neglecting the values of numerical coefficients, if the exponent of R had been 4/viii instead of three/8, and with the inclusion of units for g (gravitational dispatch), it would have had verbal homogeneity. Separately, it is noted that for Manning'due south equation to have dimensional homogeneity, the units of n in Equation ane had been historically assigned artificially equally seconds/feet^1/3 or seconds/feet^viii/24. In Equation 3, now, likewise including units for yard, n has units of seconds/feet^5/24.

It is considered that these 2 differences in Manning'due south equation and Manning's n may exist due to the uncertainty or inaccuracy of the information measurement in the limited examination flume available to the students. Therefore, again, information technology is emphasized that the concluding numerical results of this experiment probably have a degree of doubtfulness, just the method to more accurately quantify Manning'due south equation is conspicuously demonstrated.

The term S(grand) is the slope times gravitational acceleration. As the slope, d(y)/dx, becomes larger, there is a larger gravitational force acting to accelerate the menstruum.

As mentioned earlier, Manning'south equation is an average of all the open-channel equations published prior to 1889. The fact that it did not include the outcome of the velocity head correction factor is quite understandable. It was not until as late as 1877 that the Coriolis velocity head correction factor was recognized to be a variable and not a constant.

The relationships of Equation 2 prove Manning'south n is a metric for the velocity head correction factor, that is, n is proportional to α^1/2. Theoretically, if n is doubled, the velocity head correction factor is increased fourfold and the average velocity is halved. This is the mechanism through which the roughness of the fluid boundaries acts to retard the menses velocity across an infinitesimally thin cantankerous-section.

As noted, Manning's n is directly affected past the hydraulic radius (R^vii/24). This does show that selecting a Manning's n is not only a role of roughness, but of the cantankerous-exclusive shape of the water grade. The fact that canals may exhibit some differences in Manning's north due to their shape solitary, equally well as their roughness, has been previously documented in other literature.

In a paper titled "Determination of Rugosity Coefficient for Lined and Unlined Channels" published by the Karnataka Technology Research Station in India, information technology says, "Period in channels is complicated by the fact that the form of roughness elements and hence the resistance to catamenia are functions of the characteristics of aqueduct shape and alignment. These factors make upward the coefficient of rugosity or the roughness coefficient." The reason, as mentioned before, is the smaller the hydraulic radius, the greater the relative percentage of the volume of flow that is in straight contact with the given absolute roughness of the purlieus. Therefore, the greater the drag that the boundary imposes to retard the volumetric flowrate, the more than non-compatible the velocity profile becomes, as calculated by α. Thus, the smaller the hydraulic radius, the greater the energy loss. Conversely, the greater the hydraulic radius, the more the velocity profile tends to become uniform over the cross-department. Coincidently, Chezy's C is inversely proportional to R^1/viii.

The equations adult by Chezy and Manning may appear to exist very simple; however, they represent complex interactions of hydraulic parameters of fluids in open up channels. The experimental procedure presented in this commodity may be used to study these interactions. The employ of this experimental method, on the very express and narrow ground described above, suggests that the difference between Chezy'south and Manning's equations may non be as great as it appears. The real difference may exist more in the degree of dependence that each coefficient of menstruum resistance has on the velocity caput correction factor and the hydraulic radius.

— Lee H. Sheldon, PE is a hydropower engineer with l years of experience. He has published 33 technical papers and a college textbook on hydropower technology, and has worked on every federal hydroelectric project in the Pacific Northwest, among others. He was formerly a professor at OIT, where he taught hydropower applied science and fluid mechanics.

shawfainjusly.blogspot.com

Source: https://www.powermag.com/understanding-open-channel-flow-equations-for-hydro-applications/

Bagikan Artikel ini